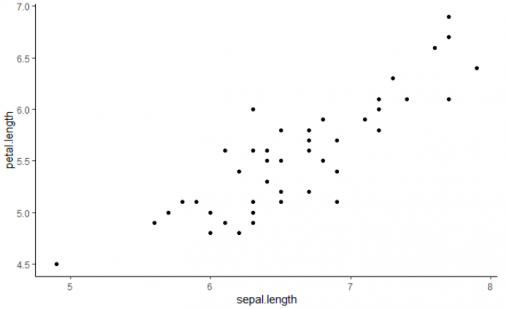
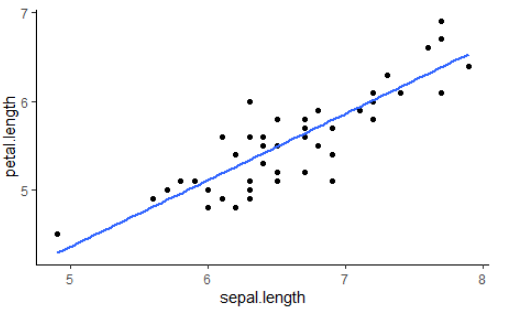
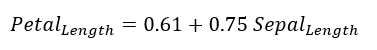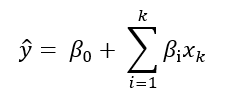Before we get into talking about linear regression, you may recall that we recently have discussed advanced machine learning techniques such as neural networks and support vector machines, but these are not always the most appropriate tool for modeling data. Machine Learning models are big, complicated, and almost impossible to interpret. While they have great capacity and are sometimes the only solution to difficult problems, their downsides can be substantial depending on what our goals are. Additionally, it is often the case that we want to understand our models or have some measures of how valid they are.

For example, the goal of a physicist may be to understand their model of a particle interaction. If they create a neural network to do this, we may have low error in the system but our human understanding of the laws of nature is no better. Likewise, an economist may be more concerned with understanding the general relationship between political uncertainty in elections, uncertainty in public policy, and uncertainty in financial markets, than creating a complex interactive system that prevents generalizations that could be applied to governance, electioneering, or market trading. So, for the time being, let us return from the vast jungles of machine learning to the tamed and comfortable community of traditional statistical models, the first of which will be linear regression.

What is Linear Regression?

Why is it called “regression?” Mostly from tradition. The term originated many centuries ago and has stuck. You may have heard of the concept of “regression to the mean.” The concept is that data may divert from an expected “average” value, but over multiple observations, it will revert or “regress” to this expected value. For example, a tall person is likely to have children that are also tall, but probably less so. They will likely “regress” towards the average height rather than being taller than their parent.

Note that regression is modeling a numeric relationship. The output of the regression is a number. This is different from something like categorization, which outputs a class or label for the input data. The second part of the name is linear, referring to the fact that in linear Regression, we only care about linear relationships; our model is just going to be the sum of things.

Let’s consider a simple example. Using the traditional Iris set of data, examine the relationship between the length of a flower’s sepal to the length of its petal for the Virginica variety. A Linear Regression would attempt to model the interaction between petal length and sepal length as a line of best fit.

From the chart below, we can see there is a general linear trend in the data. As sepal length increases, petal length increases in a similar manner. Linear regression produces a linear equation which is the model of the system.

This is a simple, interpretable form that is very useful for analysis and understanding. From the equation, we can say that for each additional centimeter of sepal length, we generally observe around 0.75 centimeters of additional petal length in a Virginica Iris.

How is a Linear Model Calculated?

By now you probably have guessed the general form of a linear regression. Our linear model is:

Our estimate for the target variable is expressed as a bias term or intercept plus a weighted sum of our input variables. This a nice linear form. But given some data, how can we create a such a model it? There are an infinite number of lines to choose from, so which is the best? We need a way to measure how good our model is. This is where the concept of error or “residuals” comes into play. For each data point, we want to measure how far from our prediction the actual data was. There are several methods for this, the most common of which is called Residual Sum of Squares (RSS). RSS is the sum of the squared residuals. A residual is the difference between the real value for our target variable and the predicted value. It is often asked why we don’t call these terms “errors” instead of “residuals”, particularly since the term “residual” seems more confusing and an excuse to use a fancy math term to sound important. Unfortunately, a full answer and explanation is beyond the scope of this article, but in short, the reason is that this difference is not actually an “error.” When creating a model, we are fully aware that there is some variance in the distribution of the target variable. The full linear model equation includes a noise term, which is a Gaussian of mean 0, with some standard deviation that is estimated by the model. Thus, “residuals” are measuring this noise, which is what remains after removing the deterministic aspect of our model. So, our RSS is:

Now that we have a measure of how our model performs, we can compare lines to choose the best one. RSS is a measure of how much variability there is in distance from our line. The best line would have the least RSS measure. Thus, to choose the line of best fit we must find this minimizing line. This sounds like a difficult task. How would we be able to find that line? We can’t test each line one by one because there are infinite lines to consider! The answer is we use a method called Ordinary Least Squares. Now at this point, we will simply wave our hands and assure you that calculus and some linear algebra will solve this problem for us algorithmically and we don’t need to worry about it.

How to Assess a Linear Model

Additionally, for each coefficient term in our model, we can calculate a p-value to determine if that estimation is statistically significant. If we encounter large p-values, we may question whether the inclusion of that variable into the model is a good idea. In those cases, the variable may not be useful and we can retry the model after discarding it. One technique is to gradually build a model by adding variables one at a time and testing to see if there is a statistically significant increase in model performance by the addition of the next variable. This technique is called AnoVa. Another method for testing our model is by analyzing the distribution of the residuals. Ideally, they should have a normal distribution and be homoscedastic; that is, they maintain roughly the same variance across the fitted values of the model and across the inputs to the model. We want the residuals to behave the same across our data because that indicates regular performance. We don’t want the model to suddenly be worse for some areas or be unpredictable.

While all this analysis is again beyond the scope presented here, it is important to understand that because of the simplicity of the linear regression model, these types of robust, interpretable, and well understood statistical analyses are possible. We can be intimately familiar with our linear models in ways that are impossible for more complex structures.

What Flexibility Exists in Linear Models?

The biggest weakness of linear regression is that it is only possible to model direct linear relationships. But there are many more types of relationships in the world that we would like to model. Luckily, there are very easy ways to inject non-linearity into linear regression. The first of which is transformations on our data. Instead of modeling our variables directly, it is very common to transform them first such as taking a logarithm of the values or some other Power transform. There may not be a linear relationship between our values directly, but there could be one between their logarithms. A model of this kind can be interpreted as saying an increase in the dependent variable by 1% implies an increase in the target variable by X%.

Another technique is to include squared terms of our variables into the model as well. We simply square our data and treat that square as another separate variable. Yet another technique is to use what are called interactions. These are treated as combinations of existing variables. For example, if we include Sex and Height into our model, we can include a term, Sex:Height, which is just the combination of the two. Essentially, this creates two new variables called Male:Height, which is the same as Height for males and 0 otherwise, and likewise for Female:Height. This interaction term can model the separate effects of Height for Males and Height for Females. Perhaps the Height term has more dramatic effects for Females than Males?

The Power of Linear Regression Models

Linear regression models are extremely popular across domains because of their robustness and simplicity. Because of transformation and other techniques, linear regression models can model a wide range of dependencies in our data. Because their form is well defined, unlike Neural Networks, they have statistical properties that we can analyze to compare models, make interpretations, and derive important information. Linear regression is not only useful for predictions, it can do what most machine learning models cannot – describe the system. If you have a numerical value you want to model, a relatively short list of independent variables to use, and a desire to understand the model you create, linear regression should usually be your first choice. Luckily, if you use PolyAnalyst, you have all of those options available to test and find out what works best for your data.